(Veröffentlicht am 9. November 2014 | Kategorie: Spiele | Schlagwörter: Brettspiele, Schach)
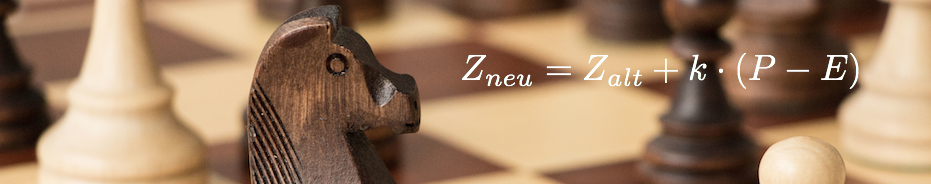
In diesem Artikel werden die ELO-Zahl, die die Stärke von Schachspielern bewertet, und die darauf basierende Berechnung des erwarteten Resultats erläutert. Diese wird beispielhaft für die Kontrahenten der Schach-WM 2014 durchgeführt.
Derzeit wird in Sotschi, Russland die FIDE Schachweltmeisterschaft 2014 zwischen Viswanathan „Vishy“ Anand und Magnus Carlsen ausgetragen.
Nach der letztjährigen Niederlage hat sich Vishy Anand im Herausfordererturnier an den Weltmeistertisch zurückgekämpft und hofft nun, Revanche zu nehmen. Neben der körperlichen Verfassung, der Vorbereitung, etc. steht vor solch wichtigen Partien die aktuelle Spielstärke im Zentrum dieser Vergleiche. Neben den Turnierergebnissen der letzten Monate und Jahre der Spieler wird hierzu die sogenannte „ELO-Zahl“ herangezogen – eine Wertungszahl, die die Spielstärke eines Spielers abbilden soll (im Folgenden bezieht sich „ELO-Zahl“ auf das FIDE-Rating).
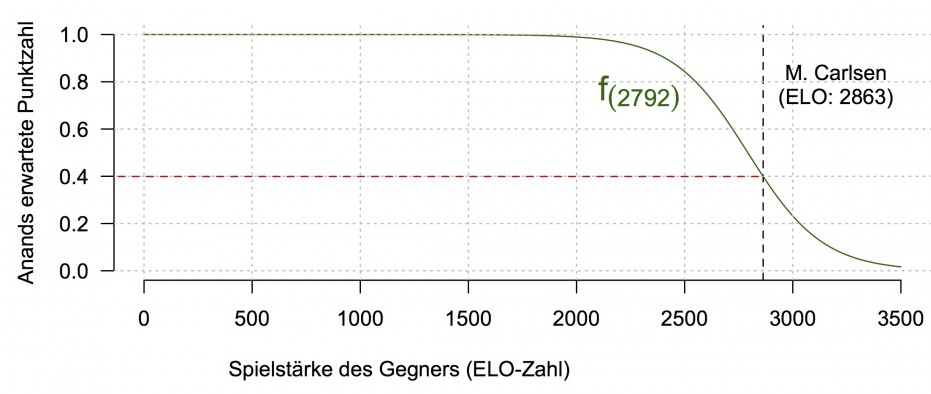
Da Carlsen eine höhere ELO-Zahl als Anand hat (2863 zu 2792), sind die Rollen im derzeitigen Duell über 12 Partien ähnlich verteilt wie bei der WM letztes Jahr – Magnus erscheint als klarer Favorit in den Augen vieler Beobachter. Im Folgenden soll daher geklärt werden, wie diese Zahlen zustandekommen, was das für die Gewinnwahrscheinlichkeiten bedeutet, wie deutlich der tatsächliche „mathematische Unterschied“ ist und was der Ausgang der Partien wiederum für die ELO-Zahl bedeutet.
Wofür braucht man aber so eine Zahl? Sie ermöglicht es zum Beispiel, den Ausgang einer Partie zwischen zwei Spielern zu bewerten. Wenn ein sehr guter und ein eher schlechter Schachspieler gegeneinander antreten, ist ein Sieg des Underdogs wesentlich unwahrscheinlicher und daher auch höher zu bewerten, als ein Sieg des Favoriten. Um die Wahrscheinlichkeiten und die Belohnung in Zahlen zu bannen, braucht man ein Bewertungssystem, das die beiden Spieler vergleicht. Natürlich will man auch wissen, wer der beste ist – ohne vielleicht andauernd die wahrscheinlich weltbesten Spieler gegeneinander antreten zu lassen. Und genau das leistet das ELO-Rating.
Jede Schachspielerin und jeder Schachspieler bekommt eine ELO-Zahl. Die ELO-Zahl ist eine positive natürliche Zahl und stellt ein Maß für die Spielstärke eines Spielers dar – was für zwei beliebige Spieler nun einen Vergleich der Leistungsstärke zulässt. Zu Beginn der Spielerlaufbahn wird die ELO-Zahl durch Vergleiche mit anderen ELO-gerateten Spielern geschätzt. Durch jede Schachpartie, die ein Spieler spielt, verändert sich nun seine ELO-Zahl und nähert sich seiner relativen Leistung (im Vergleich zu allen anderen eingestuften Spielern) an.
Veränderung der Spielstärke
Der notwendige Grundmechanismus des ELO-Ratings ist das ständige Messen der eigenen Leistung mit anderen. Dadurch aktualisieren sich die ELO-Zahlen ständig und bilden die relative Leistung zu allen anderen ELO-Zahl-Trägern ab. Im Folgenden ist der Grundmechanismus, die Aktualisierung, anhand eines Beispiels Schritt für Schritt erklärt.
Steht eine Schachpartie an, wird der Spielausgang auf der Basis der ELO-Zahlen beider Spieler errechnet. Bei einem Sieg erhält der Gewinner einen, der Verlierer keinen Punkt. Bei einem Remis (Unentschieden) erhalten beide Spieler 0,5 Punkte.
Als Beispiel soll der Weltmeisterschaftskampf dienen. Daher betrachten wir die ELO-Zahlen von Viswanathan Anand (
) und Magnus Carlsen (
). Für die Bestimmung des erwarteten Ausgangs wählt man eine Funktion, die u.a. den folgenden Eigenschaften entspricht:
Diese und weitere Eigenschaften führten zur Wahl eines logistischen Ansatzes. Wichtig für die weitere Berechnung ist Tatsache, dass Schachspiele unentschieden ausgehen können. Daher wird die Wahrscheinlichkeit, dass ein Spiel unentschieden ausgeht, halbiert und zu den Gewinnwahrscheinlichkeiten der beiden Spieler addiert. Der durchschnittliche erwartete Ausgang 
für Vishy Anand und 
für Magnus Carlsen in einem Spiel berechnen sich demnach mit folgenden Formeln:
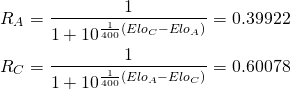
Unten ist Anands derzeitige Erwartungskurve 
abgebildet. Sie zeigt sein erwartetes Resultat in Abhängigkeit der ELO-Zahl seines Gegners.
Für die WM 2014 bedeutet das also: Werden tatsächlich 12 Partien gespielt, wäre das erwartete Ergebnis durch 
und 
bestimmt:
Magnus Carlsen (7.0) – Viswanathan Anand (5.0)
Wie es nach der WM mit den ELO-Zahlen der beiden Kontrahenten weitergeht, was die Formel im Header bedeutet und Anmerkungen zum Modell der ELO-Zahlen folgen im Artikel: Die ELO-Zahl – Teil 2.
Quelle der ELO-Stände:
– http://ratings.fide.com/ abgerufen am 09.11.2014
Erschienen in der Kategorie: Spiele
27. November 2014 um 14:26
Da hast du/die Mathematik das Endergebnis recht genau vorrausgesagt. Danke. Ich freu mich auf Teil 2