
(Veröffentlicht am 20. März 2013 | Kategorie: Spiele | Schlagwörter: Doppelkopf, Hochzeit, Kartenspiele)

Als Fortsetzung des Artikels ‚Das Hochzeitsproblem – Teil 1‘, der Spiele mit 40 oder 48 Handkarten betrachtet, wird die Wahrscheinlichkeit für das Auftreten einer möglichen Hochzeit im Doppelkopf nun für eine beliebige Zahl von Handkarten untersucht.
Eine mögliche Hochzeit liegt dann vor, wenn ein Spieler beide Kreuzdamen auf der Hand hat. Zunächst wird jedoch die im Vorgänger-Artikel erarbeitete Formel vereinfacht und inhaltlich umgedeutet.
Als Ergebnis der Betrachtungen zur Wahrscheinlichkeit einer möglichen Hochzeit schloß der erste Teil mit der Formel
![]()
wobei ![]() die Zahl der Gesamt-Karten und
die Zahl der Gesamt-Karten und ![]() die Anzahl der Hand-Karten eines Spielers angibt. Diese Notation wird aus inhaltlichen Gründen beibehalten, obwohl in allen betrachteten Fällen
die Anzahl der Hand-Karten eines Spielers angibt. Diese Notation wird aus inhaltlichen Gründen beibehalten, obwohl in allen betrachteten Fällen ![]() gilt (was wir gleich in der folgenden Rechnung verwenden werden).
gilt (was wir gleich in der folgenden Rechnung verwenden werden).
Mit der üblichen Definition des Binomialkoeffizienten gilt dann, mit genügend großen ![]() und
und ![]() , sowie
, sowie ![]() :
:
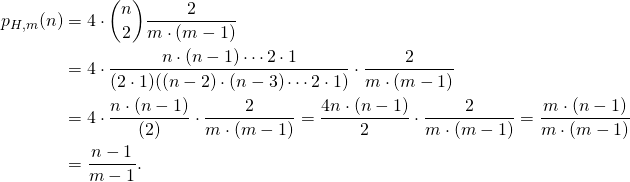
Damit lässt sich also die Wahrscheinlichkeit sehr viel einfacher berechnen. Inhaltlich heißt das soviel wie: „Nimm eine Kreuzdame auf die Hand. Jetzt hast Du noch ![]() Möglichkeiten, von
Möglichkeiten, von ![]() übrigbleibenden Karten die verbleibende Kreuzdame zu ziehen.“ Eine schöne Vereinfachung.
übrigbleibenden Karten die verbleibende Kreuzdame zu ziehen.“ Eine schöne Vereinfachung.
Offensichtlich, und das ist kein sofort einsichtiges Ergebnis des ersten Artikels, wird die Wahrscheinlichkeit für eine mögliche Hochzeit mit steigender Gesamtkartenanzahl höher. Die Wahrscheinlichkeit bei insgesamt 12 Karten ist ![]() , bei 40 Karten
, bei 40 Karten ![]() und bei 48 Karten
und bei 48 Karten ![]() .
.
Es – oder zumindest mir – stellt sich die Frage: Wie verhält sich die Wahrscheinlichkeit wenn man die Anzahl der Gesamtkarten immer weiter erhöht. Dabei wird die Spieleranzahl (4) und die Anzahl der Karten, die auf einer Hand sind (nämlich 2 Kreuzdamen – man könnte auch fragen, was wäre bei 3 Karten auf einer Hand, etc.), konstant gehalten.
Dazu sind hier die genannten Wahrscheinlichkeiten für alle möglichen Handkartenanzahlen (durch 4 teilbar) in einem Koordinatensystem dargestellt.
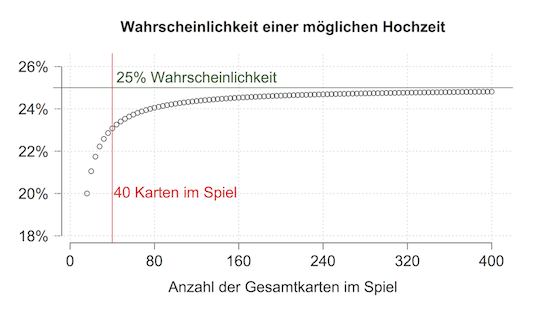
Falls es also nicht mit dem Teufel zugehen sollte, wird beim Spiel mit unendlich vielen Gesamtkarten die Wahrscheinlichkeit für eine mögliche Hochzeit bei 25 % liegen.
Um das zu verifizieren folgen zwei Betrachtungen. Erstens – die Zahlenfolge ist monoton wachsend. Erhöht man die Gesamtzahl der Karten um 4 wird eine Hochzeit wahrscheinlicher. Denn für ![]() (also eine Handkarte) und
(also eine Handkarte) und ![]() gilt:
gilt:
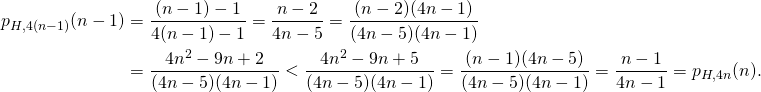
Zweitens – der Grenzwert der Folge ist ![]() .
.
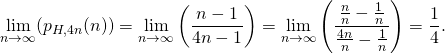
Spielt man also mit unendlich vielen Karten, so tritt eine mögliche Hochzeit mit der Wahrscheinlichkeit von 25 % ein. Aber wenn, dann für ne längere Zeit…
Erschienen in der Kategorie: Spiele